介绍

斐波那契搜索 (Fibonacci search) ，又称斐波那契查找，是区间中单峰函数的搜索技术。

原理

斐波那契搜索就是在二分查找的基础上根据斐波那契数列进行分割的。在斐波那契数列找一个等于略大于查找表中元素个数的数 F [n]，将原查找表扩展为长度为 F[n] (如果要补充元素，则补充重复最后一个元素，直到满足 F [n] 个元素)，完成后进行斐波那契分割，即 F [n] 个元素分割为前半部分 F [n-1] 个元素，后半部分 F [n-2] 个元素，找出要查找的元素在那一部分并递归，直到找到。

描述

斐波那契查找是依据斐波那契序列的特点对表进行分割的。假设开始时表中记录的个数 (不妨设为 n) 比某个斐波那契数 (Fu) 小 1，即 n = Fu - 1（这也是一个前提条件），然后将给定值 key 和 a [Fu-1] 进行比较。

• 若相等，则查找成功。
• 若 key <a [Fu-1] ，则继续在 a [1] 至 a [Fu-1 - 1] 的子表中进行查找。
• 若 key > a [Fu-1] ，则继续在 a [Fu-1 + 1] 至 a [Fu - 1] 的子表中进行查找。该子表的长度为 Fu-2 - 1。

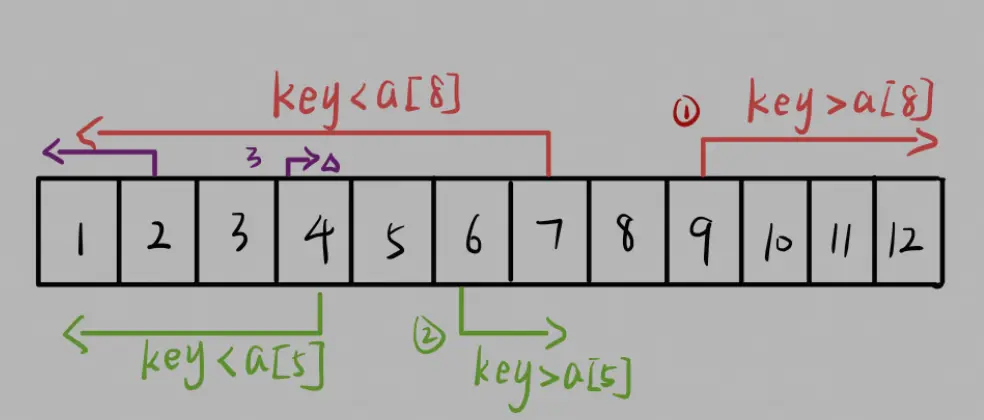
步骤如下：

• 首先我们生成一个斐波那契数列： F1 = 1, F2 = 1， F3 = 2， F4 = 3， F5 = 5， F6 = 8， F7 = 13；
• 然后我们设，有序表 a, 从 a [1]~a [12] 的值为 1 ~ 12。（为了方便理解，储存该表的数组的 a [0] 为空）
• 我们假定，需要查找的数为 key = 4。
• 因为 n = Fu - 1 ，可以知道此时，u = 7。将 key 和 a [F7-1] （即 a [8]）进行比较，我们发现 key<a[8] 。
• 然后在 a [1]~a [7] 中进行查找，此时 u = 6。将 key 和 a [F6-1]（即 a [5]）进行比较，我们发现 key<a[5] 。
• 然后再 a [1]~a [4] 中进行查找，此时 u = 5。将 key 和 a [F5-1]（即 a [3]）进行比较，我们发现 key>a[3] 。
• 此时只剩 a [4]，查找完毕。

斐波那契数列

// 递归法
const Fn = (n) => {

    // 容错：字符串可转为数字类型
    if(typeof n === 'string' && n !== '') { console.info(`n: ${n} 是字符串，将会自动转化为数字类型: ${+n}`); n = +n; }

    // 类型判断
    if (typeof n !== 'number') { return console.error(`n: ${n} 必须为数字类型`); }

    // 容错：浮点数能转成整数进行计算
    if (!isNaN(n) && n !== parseInt(n)) { console.info(`n: ${n} 不是整数，将会自动转化为整数: ${parseInt(n)}`); n = parseInt(n); }

    // 范围判断
    if (n < 0 || isNaN(n)) { return console.error(`n: ${n} 必须大于0，并且不能为NaN`); }

    if(n === 0) { return 0; }

    if(n === 1) { return 1; }

    return Fn(n - 1) + Fn(n - 2);
}

// 迭代法
const Fn = (n) => {

    // 容错：字符串可转为数字类型
    if(typeof n === 'string' && n !== '') { console.info(`n: ${n} 是字符串，将会自动转化为数字类型: ${+n}`); n = +n; }

    // 类型判断
    if (typeof n !== 'number') { return console.error(`n: ${n} 必须为数字类型`); }

    // 容错：浮点数能转成整数进行计算
    if (!isNaN(n) && n !== parseInt(n)) { console.info(`n: ${n} 不是整数，将会自动转化为整数: ${parseInt(n)}`); n = parseInt(n); }

    // 范围判断
    if (n < 0 || isNaN(n)) { return console.error(`n: ${n} 必须大于0，并且不能为NaN`); }

    let pre = 0,
        next = 1,
        result;

    if (n === 0) { result = pre; }

    if (n === 1) { result = next; }

    while (n >= 2) {
        n--;
        result = pre + next;
        pre = next;
        next = result;
    }

    return result;
};

实现

JavaScript

/****************************************************************************
 * This implementation is based on Generalizing the Fibonacci search we
 * define the Fibonacci search of degree K. Like the Fibonacci search,
 * which it reduces to for K = 2, the Fibonacci search of degree K
 * involves only addition and subtraction.
 *
 * We define a function fibonacciSearch() that takes an array of numbers,
 * the item (number) to be searched for and the length of the items in the array
 ****************************************************************************/

const fibonacciSearch = (arr, x, n) => {
  let fib2 = 0 // (K-2)'th Fibonacci Number
  let fib1 = 1 // (K-1)'th Fibonacci Number.
  let fibK = fib2 + fib1 // Kth Fibonacci

  /* We want to store the smallest fibonacci number smaller such that
    number is greater than or equal to n, we use fibK for this */
  while (fibK < n) {
    fib2 = fib1
    fib1 = fibK
    fibK = fib2 + fib1
  }
  //  This marks the eliminated range from front
  let offset = -1

  /* while there are elements to be checked. We compare arr[fib2] with x.
    When fibM becomes 1, fib2 becomes 0 */

  while (fibK > 1) {
    // Check if fibK is a valid location
    const i = Math.min(offset + fib2, n - 1)

    /*  If x is greater than the value at
      index fib2, Partition the subarray array
      from offset to i */
    if (arr[i] < x) {
      fibK = fib1
      fib1 = fib2
      fib2 = fibK - fib1
      offset = i
      /* If x is greater than the value at
            index fib2, cut the subarray array
            from offset to i */
    } else if (arr[i] > x) {
      fibK = fib2
      fib1 = fib1 - fib2
      fib2 = fibK - fib1
    } else {
    //  return index for found element
      return i
    }
  }

  //    comparing the last element with x */
  if (fib1 && arr[offset + 1] === x) {
    return offset + 1
  }
  //    element not found. return -1
  return -1
}

参考

• Fibonacci search technique - Wikipedia (opens new window)
• 斐波那契搜索_百度百科 (opens new window)