介绍

快速选择（英语：QuickSelect）是一种从无序列表找到第 k 小元素的选择算法。它从原理上来说与快速排序有关。与快速排序一样都由托尼・霍尔提出的，因而也被称为霍尔选择算法。同样地，它在实际应用是一种高效的算法，具有很好的平均时间复杂度，然而最坏时间复杂度则不理想。快速选择及其变种是实际应用中最常使用的高效选择算法。

原理

快速选择的总体思路与快速排序一致，选择一个元素作为基准来对元素进行分区，将小于和大于基准的元素分在基准左边和右边的两个区域。不同的是，快速选择并不递归访问双边，而是只递归进入一边的元素中继续寻找。这降低了平均时间复杂度，从 O (n log n) 至 O (n)，不过最坏情况仍然是 O (n2)。

与快速排序一样，快速选择一般是以原地算法的方式实现，除了选出第 k 小的元素，数据也得到了部分地排序。

复杂度

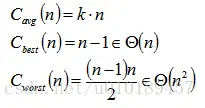
实现

JavaScript

/*
 * Places the `k` smallest elements in `array` in the first `k` indices: `[0..k-1]`
 * Modifies the passed in array *in place*
 * Returns a slice of the wanted elements for convenience
 * Efficient mainly because it never performs a full sort.
 *
 * The only guarantees are that:
 *
 * - The `k`th element is in its final sort index (if the array were to be sorted)
 * - All elements before index `k` are smaller than the `k`th element
 *
 * [Reference](http://en.wikipedia.org/wiki/Quickselect)
 */
function quickSelectSearch (array, k) {
  if (!array || array.length <= k) {
    throw new Error('Invalid arguments')
  }

  let from = 0
  let to = array.length - 1
  while (from < to) {
    let left = from
    let right = to
    const pivot = array[Math.ceil((left + right) * 0.5)]

    while (left < right) {
      if (array[left] >= pivot) {
        const tmp = array[left]
        array[left] = array[right]
        array[right] = tmp
        --right
      } else {
        ++left
      }
    }

    if (array[left] > pivot) {
      --left
    }

    if (k <= left) {
      to = left
    } else {
      from = left + 1
    }
  }
  return array
}

参考

• 快速选择 - 维基百科，自由的百科全书 (opens new window)